Boolesche Algebra

Die bool'sche Operatoren

Konjunktion (AND)

Die Konjunktion ist eine der grundlegenden logischen Verknüpfungen der Aussagenlogik. Die Konjunktion zweier Aussagen A und B ist genau dann wahr, wenn sowohl A und B wahr sind. Das mathematiche Symbol ist ∧. In Java wird das AND durch && repräsentiert.

A	B	A ∧ B
false	false	false
false	true	false
true	false	false
true	true	true

Disjunktion (OR)

Die Disjunktion ist eine der grundlegenden logischen Verknüpfungen der Aussagenlogik. Die Disjunktion zweier Aussagen A und B ist genau dann wahr, wenn mindestens eine der Aussagen A oder B wahr ist. Das mathematische Symbol ist ∨. In Java wird das OR durch || repräsentiert.

A	B	A ∨ B
false	false	false
false	true	true
true	false	true
true	true	true

Venn-Diagramm?

Negation (NOT)

Die Negation ist eine wichtige Operation in der Aussagenlogik. Die Negation einer Aussage A führt zur ihrer Verneinung, d.h. aus einer wahren Aussage wird eine falsche Aussage und umgekehrt. Das mathematische Symbol ist ¬. In Java wird das NOT durch ! repräsentiert.

A	¬A
false	true
true	false

Kontravalenz (XOR)

Die Kontravalenz ist eine erweiterte logische Verknüpfung in der Aussagenlogik. Die Kontravalenz zweier Aussagen A und B ist genau dann wahr, wenn entweder A oder B, aber nicht beide wahr sind. Das mathematische Symbol ist ⊕. In Java wird das XOR durch ^ repräsentiert.

A	B	A ∨ B
false	false	false
false	true	true
true	false	true
true	true	false

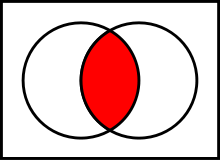
Venn-Diagramm?

Implikation

Die Implikation ist eine erweiterte logische Verknüpfung in der Aussagenlogik. Die Implikation zweier Aussagen A und B ist genau dann wahr, wenn A falsch oder B wahr ist. Das mathematische Symbol ist ⇒. Die Implikation ist [semantisch äquivalent] zu ¬A ∨ B. In Java gibt es keinen Implikationsoperator. Eine Implikation wird meistens durch "wenn A, dann B" im Deutschem ausgedrückt.

A	B	A ⇒ B
false	false	true
false	true	true
true	false	false
true	true	true

Venn-Diagramm?

Äquivalenz (XNOR)

Die Äquivalenz ist eine erweiterte logische Verknüpfung in der Aussagenlogik. Die Äquivalenz zweier Aussagen A und B ist genau dann wahr, wenn A und B wahr oder A und B falsch sind. Das mathematische Symbol ist ⇔. Die Äquivalenz ist [semantisch äquivalent] zu A ∧ B ∨ ¬A ∧ ¬B. In Java gibt es keinen Operator hierfür. Die Äquivalenz wird meistens durch "genau dann A, wenn B" im Deutschem ausgedrückt.

A	B	A ⇔ B
false	false	true
false	true	false
true	false	false
true	true	true

Venn-Diagramm?

Peano-Axiome (erweitertes Wissen)

Kommutativgesetze

(1) A ∧ B ≡ B ∧ A

(1') A ∨ B ≡ B ∨ A

Assoziativgesetze

(2) (A ∧ B) ∧ C ≡ A ∧ (B ∧ C)

(2') (A ∨ B) ∨ C ≡ A ∨ (B ∨ C)

Idempotenzgesetze

(3) A ∧ A ≡ A

(3') A ∨ A ≡ A

Distributivgesetze

(4) A ∧ (B ∨ C) ≡ (A ∧ B) ∨ (A ∧ C)

(4') A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C)

Neutralitätsgesetze

(5) A ∧ true ≡ A

(5') A ∨ false ≡ A

Extremalgesetze

(6) A ∧ false ≡ false

(6') A ∨ true ≡ true

Doppelnegationsgesetz

(7) ¬¬A ≡ A

De Morgansche Gesetze

unwichtig?

Komplementärgesetze

(8) A ∧ ¬A ≡ false

(8') A ∨ ¬A ≡ true

Dualitätsgesetze

unwihtig?

Absorptionsgesetze

unwichtig?